Tech Article | 23/02
Electricity instead of gas for higher energy efficiency
It is widely held that you should “never change a running system”, but how can you improve a system if you aren’t allowed to change it? Conventional processes certainly have their historically grown legitimacy, but it can be worthwhile to question the status quo in order to further improve functioning processes and/or save costs.

A running process with glass
Maybe you have it next to you on the table right now: a glass bottle with a drink. This glass, which keeps your drink from spilling all over the table, was once produced in a glassworks. For this purpose, suitable raw materials (e.g., quartz sand) or even glass fragments from used glass containers are brought to very high temperatures above the melting point and finally melted down into a homogeneous mass. Small portions of this molten mass are placed in molds, where they are shaped into their final form and cooled back down to room temperature.
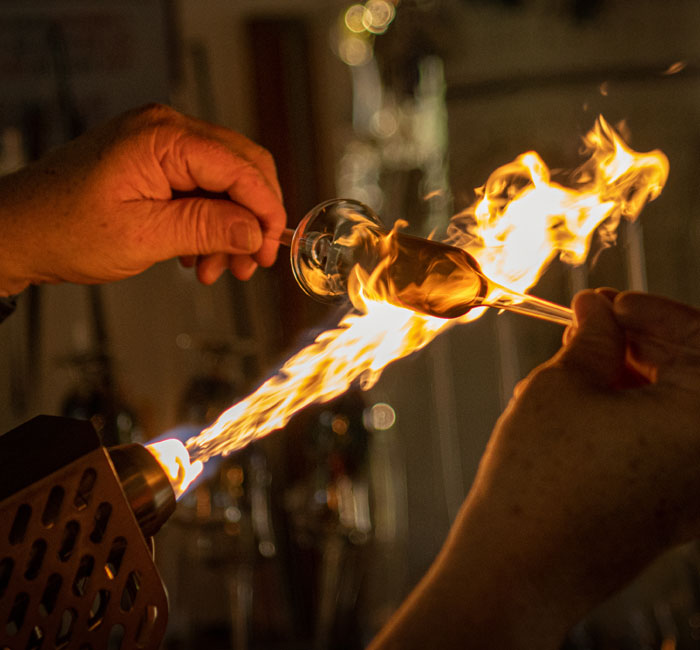
To achieve these high temperatures within the glass melt, fossil fuels are burned, and the thermal energy released is transferred to the glass via convection and radiation. This process has been working for centuries with coal/coke and nowadays in large industrial plants mainly with gas. Today, however, it’s no secret that these fossil forms of energy are becoming increasingly scarce and correspondingly more expensive – not to mention the negative environmental impact. Optimization potentials must therefore be identified in order to make the process more efficient.
Can electricity replace gas?
A very efficient heating option in manufacturing processes is provided by an electrical or electromagnetic power supply. Here, power can be very precisely introduced into the component to be heated, without major thermal losses. Such processes have already become a fixture, especially in the metalworking industry, and are continuing to spread far beyond.
Compared to metals, glass has one somewhat important disadvantage: At room temperature, the electrical conductivity of glass is so low that heating via electrical and electromagnetic sources does not work. However, above a high temperature of roughly 1000°C, glass becomes an ion conductor. The electrical conductivity is still significantly below that of metals but is sufficient to allow an electric current flow and thus ultimately generate heat in the glass directly via electrical power.
So, there is no clear answer to the question "Can electricity replace gas?" It still needs a starting process, which is realized by a gas flame. As soon as an electric current is built up, the process COULD basically be run with electric energy alone. New cold materials are melted via heat conduction and if the process can be run continuously, it would be theoretically conceivable. But there are still things like "maintenance", "batch change", "malfunctions", etc., which throw a wrench in the works of the perfect electrical world.

Electric or not electric...
... that could be the appropriate question here. If you change the location and type of power input in your process, then of course the temperature distribution also changes, and this temperature distribution is ultimately decisive for the process. However, this in turn raises the question HOW the temperature distribution changes.
Particularly in highly aggressive glass melts, measurement with thermocouples and/or flowmeters is difficult. However, numerical simulation is suitable for analyzing the extent to which the temperature profile and thus also the process behave when the power input is changed. This makes it possible to evaluate the scalar and vector quantities at any location at any time – even without the influence that would occur through the insertion of a measuring instrument. In addition, electrics and temperature influence each other, which is why the simulation should be carried out in a coupled manner in order to generate useful results.

Electrical or thermal? No, both!
The process mentioned here includes both electrical and thermal effects, which further influence each other. Heat flow from a gas flame in cooperation with electrical losses of the current supply determine the temperature field. To meet all these requirements, Ansys offers the "Coupled Field" system with the necessary boundary conditions and loads.
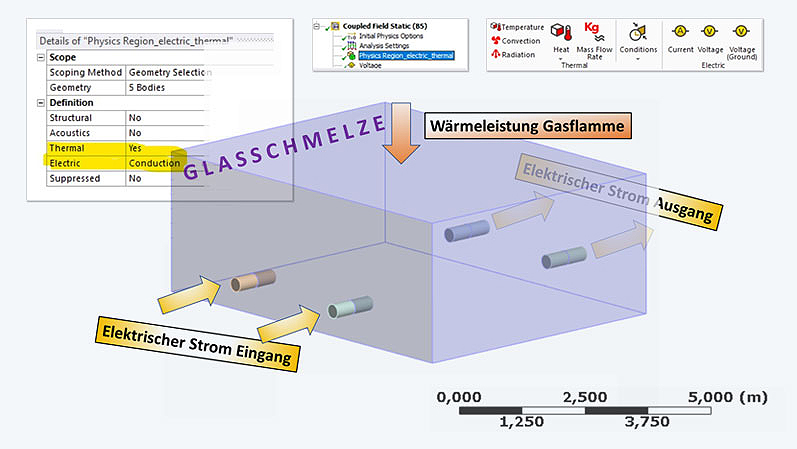
By the way: Compared to the "Thermal Electric" system, the "Coupled-Field" systems additionally offer the consideration of a mass transport... or the analysis of mechanical effects... or the consideration of acoustic phenomena. Simply select the domains of your wish list within the Physics region and let's go!
Speaking of coupling: Within simulation, a distinction is made between weak coupling and strong or matrix coupling. In weak coupling, the sub-disciplines work sequentially. In our example, the electrical matrix would be solved first, and the power density evaluated. This power density would then be the input for the thermal calculation. The temperature field would be calculated and returned to the electrical system to adjust the material data. The "coupled-field" system uses strong coupling. With strong coupling, the respective dependencies are built into the matrix, so a convergent solution for both sub-disciplines must be achieved SIMULTANEOUSLY.
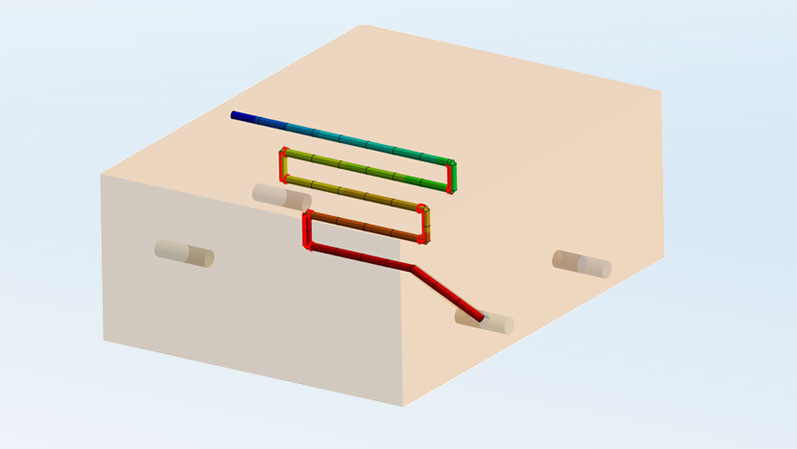
The task now is to determine the best possible ratio between conventional and electrical heating, taking into account all mutual influences and effects. Using a demonstrator model, qualitative studies can be carried out to determine the relationships between input (temperature of the gas flame, mass flow of the glass, electrical voltage at the electrodes) and output variables (temperature at the pouring point, gas power, electrical power).
School knowledge in practice!
The input of thermal energy from the gas flame occurs via radiation and convection. The third part via conduction may, for the most part, be neglected. Especially for more complex structures, the radiation solver can lead to long calculation times. A small tip: a temperature-dependent convection boundary condition, which takes "normal" convection and radiation into account, can help here. According to Newton's law, the heat flux density for convection is: q=α∙Δϑ. For the Stefan-Boltzmann law, if a radiation exchange with other surfaces may be neglected, the relation looks like this: q=σ∙ε∙(T4 - TU4 ) – with T as absolute temperature.
The total heat flux density is the sum of both mechanisms acting parallel to each other. If one now falls back on one's school knowledge and remembers the "3rd binomial formula", then one recognizes:
q=σ∙ε∙(T4 - TU 4 )=σ∙ε∙(T2 + TU 2)∙(T2 - TU2 )
If you use this procedure again, you get:
q=σ∙ε∙(T4 - TU4 )=σ∙ε∙(T2 + TU2 )∙(T + TU)∙(T - TU )
The last bracket thus represents the temperature difference, as it also occurs in Newton's law. The entire factor in front of it would thus function as an effective, temperature-dependent convection coefficient in order to take radiation effects into account.
For our simple demonstrator, we use a heat flux to describe the gas performance, an exemplary path of the introduced material to the pour point, and four electrodes: two with positive potential, two with zero potential. The outer sides of the furnace are comparatively cold thanks to good thermal insulation, so a radiation boundary condition is not necessary; only a simple convection boundary condition is used here, but this is not listed in the figure to preserve clarity.
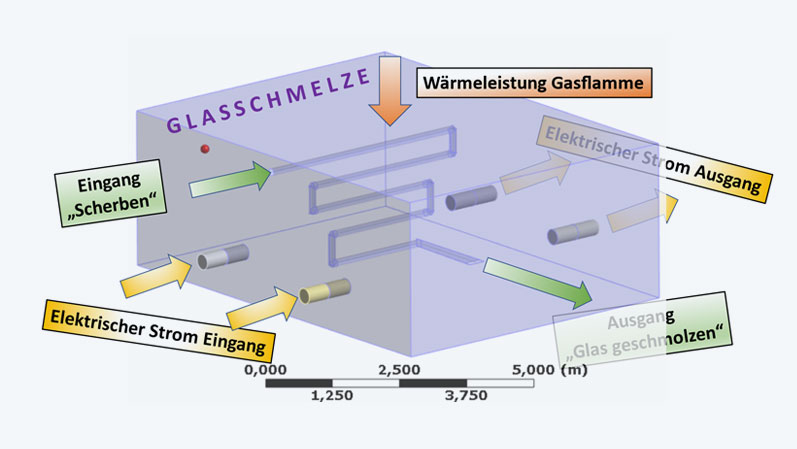
Quod erat demonstrandum!
Now we are looking for the ideal ratio of gas and electricity, and we start with the extremes, where one part is completely switched off. The goal is a temperature of 1400 °C at the nozzle.
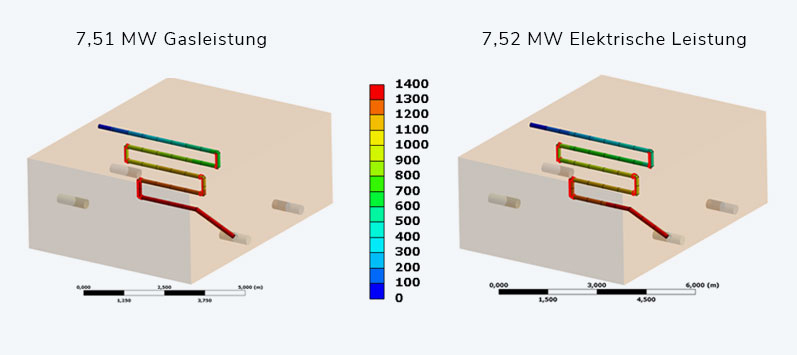
Whereas gas power causes earlier heating in the throughput direction due to the local proximity to the gas flame acting above, electrical power works in particular at the critical location of the casting. Integrally, however, equal power is required to bring the glass to the necessary 1400°C.
Using certain parameter variations, the following power balance results in the space marked out by the extrema for reaching 1400°C:
| Power in MW | ||||||
| Gas Flame | 7,51 | 4,41 | 3,45 | 2,41 | 1,24 | 0 |
| Electric Current | 0 | 1,57 | 3,07 | 5,08 | 6,27 | 7,52 |
| Total Power | 7,51 | 7,51 | 7,48 | 7,46 | 7,51 | 7,52 |
At this point it should be mentioned that other losses of the heat supply are not considered and only the power provided for heating is defined. While in reality the electricity has low feed losses, the power of the gas flame lost via the "chimney" accounts for a considerable share.
Ultimately, it becomes clear that it does not matter to the temperature field whether heating is carried out by means of gas or electricity, as long as the same total power reaches the melt. This means that the user is free to choose the proportion of gas and electricity used in the process, but from an economic point of view all efficiencies from primary energy to useful energy must of course be taken into account. Given the enormous price fluctuations on the energy market, there is huge potential for savings here - and these savings could quickly be converted into some of the beverage bottles, one of which may still be sitting on your desk.
Author

Published: July 2023
Editorial
Dr.-Ing. Marold Moosrainer
Head of Professional Development
Cover images
Left: © CADFEM Germany GmbH
Right: © Adobe Stock



