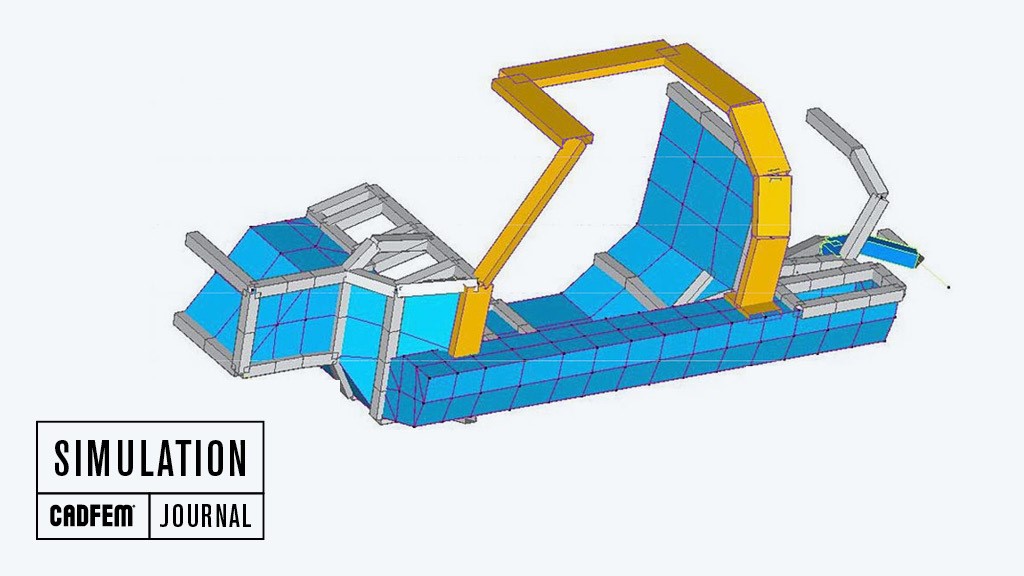
Berkeley – home of the finite element method
The origins of the finite element method
FEM simulations play their part in the production development process by assisting the user at an early stage to assess whether the essential requirements have been met and to ensure that they are fulfilled.
Questions regarding what lies at the heart of such simulations and of how the associated mathematics developed and came to be applied may never have crossed the mind of today’s computational engineers – and they may never have even heard anything about such matters. The following provides a brief overview of where it all began and of the historical development of the finite element method, giving due regard to Berkeley, which played a significant role in its development.
Ray W. Clough of the University of California coined the term “finite element method” and, along with John H. Argyris of Imperial College, London, and Stuttgart Technical University, he is considered the inventor of the finite element method.
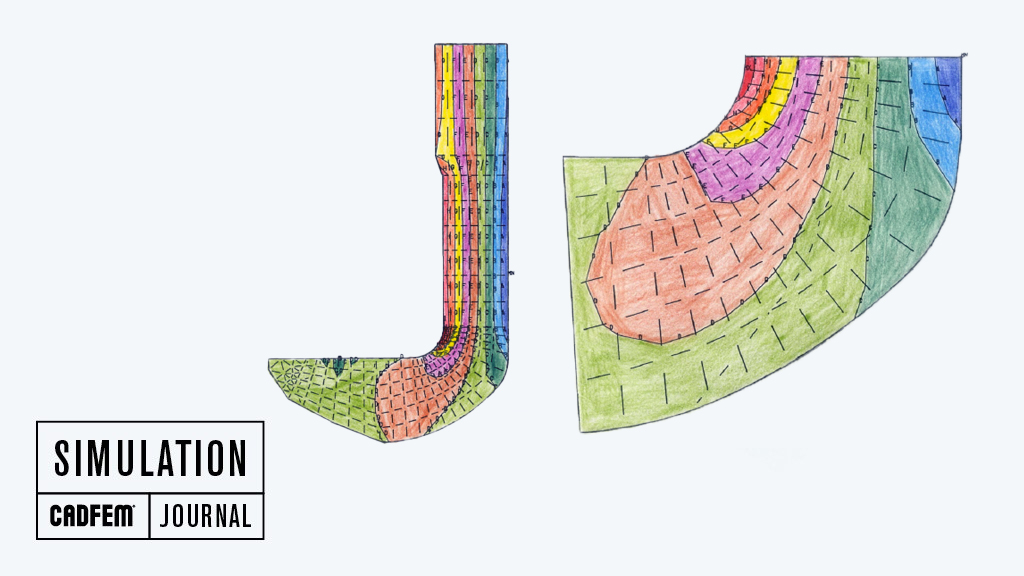
Definition / Foundations
The finite element method allows the suitability of products to be checked via the medium of a computer screen before they are ever built; it also permits the required changes to be implemented both quickly and cheaply. Engineers are interested in determining in advance how buildings, vehicles, machines, and products will behave in certain load scenarios. When building a bridge, for example, engineers want to know whether the structure will be able to support its own weight or an imposed load or whether it will be able to withstand gusts of wind or earthquakes. They would want a newly developed clothes iron to heat up as evenly and as quickly as possible. Lifting magnets need to generate magnetic fields that are strong enough to produce the desired forces. When it comes to micropumps, it is the internal flow conditions that are of interest.
The physical behavior of structures can be described mathematically using differential equations developed back in the 17th and 18th centuries. For example, von Cauchy’s theory of elasticity provides the differential equation for flexural beams – and hence also the deformation and stress caused by external loads. Laplace’s equation provides a method for describing temperature fields, and the Navier-Stokes equations capture the flow behavior of a fluid. Maxwell’s equations describe electromagnetic fields, and the Helmholtz equation deals with problems in acoustics.
Numerical approximation methods
Differential equations can be solved using either analytical or numerical methods. While analytical solutions are appropriate for straightforward academic purposes, when it comes to the diverse – and generally complex – problems relating to real-world situations, it is only numerical methods of approximation that are worth considering. Two approaches were developed along these lines: the finite difference method and the variational method. The finite difference method returns an approximate solution to a differential equation by dividing any given structure into a grid. This approach has not gained widespread acceptance.
Variational methods are based on an approximating function consisting of a set of freely chosen trial functions multiplied by unknown parameters. The approximating function’s unknown parameters are determined using a minimization principle (the minimum mean square error, or the energy minimum). This transforms the differential equation problem into a set of algebraic simultaneous equations for given unknown parameters. The quality of the approximate solution depends on the trial function employed and the number of unknown parameters.
The finite element method represents one such numerical method, though it is distinctive in that the trial functions are selected in a piecewise (element-based) manner, and the free parameters constitute physically interpretable variables located at the junction points (nodes) of the domains (elements); these variables might be displacements, temperatures, or magnetic potential, for example. The finite element method has gained wide acceptance as a computational method in that it is tailored to computers, increasing its potential. Having the simulation models divided into several domains (elements) means complex geometries can be mapped and more basic trial functions can be employed. A comprehensive description of the finite element method is found in [1].
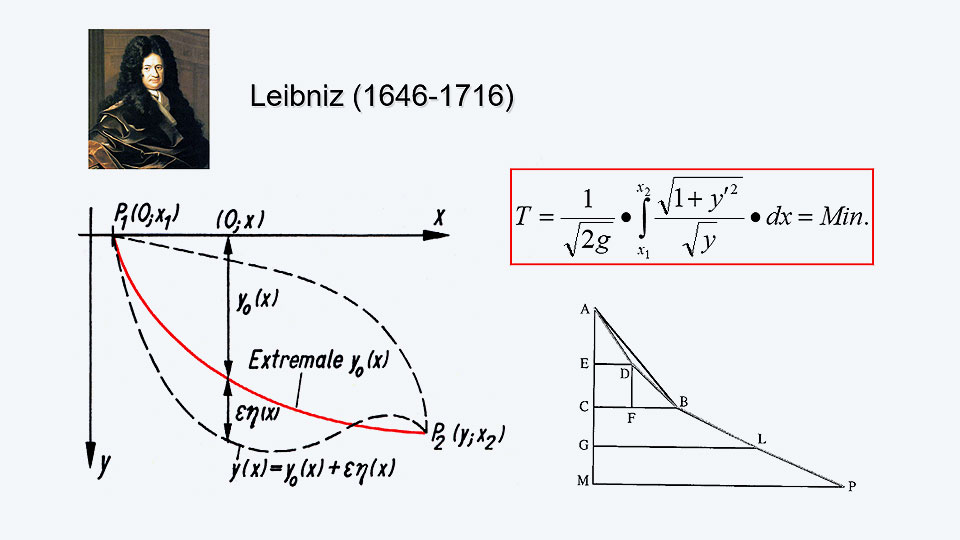
By the way, the idea that you could obtain approximate solutions through use of basic area-by-area – i.e., domain-based – functions was well-known in ancient Greece. Back then, Archimedes of Syracuse (287-212 B.C.) determined the ratio of the circumference of a circle to its diameter – i.e., pi – by approximating the shape of a circle using straight lines. The more straight sections (domains) adopted, the more accurate the result. Moving forward to 1697, Gottfried Leibniz solved the brachistochrone problem by means of approximation, using straight lines.
The historical development of the finite element method
The development of the finite element method began in the mid 1950s at various universities, though it mainly occurred at the University of California, Berkeley, the University of Wales, Swansea, and at University of Stuttgart. The University of Stuttgart was, and remains, one of the leading research institutes in the field of numerical simulation. In 2019, University of Stuttgart was granted the status of possessing the only two existing Clusters of Excellence within the field of simulation.
Between 1954 and 1956, John Argyris, Professor at both Imperial College, London, and University of Stuttgart formulated the classical force method of structural design (cf. the principle of virtual work, by Johann Bernoulli, 1667-1748) for one-dimensional rigid frames using matrix notation, in a modular and computer-compatible form. The principle of virtual work states that if a body is in equilibrium and it is subjected to a small, virtual displacement, the work is equal to zero, i.e., the potential energy is at a minimum. Rather than looking at the overall structure, Argyris used matrices to describe the relationship between the forces and the deformation at the nodes of individual bars while preserving both conditions of force equilibrium and geometric conditions – and incorporated these matrices into an overall matrix. This produces a system of equations in which the displacement values are the unknown quantity. To put it succinctly, his research into the “matrix displacement method” was published in 1960 [2]. It was later established that, from the perspective of mathematics, Argyris’ underlying physically-defined principles of the conservation of energy are, in fact, variational methods.
Erwin Stein, Ekkehard Ramm and, later on, Wolfgang A. Wall and Manfred Bischoff of the Institute for Structural Design also helped shape the development of the finite element method. From the outset, the focus was on variational methods, with several doctoral theses being completed since the 1970s on the further development of the variational methods (i.e., discretization and formulation within the FEM) that had been established by Ritz (1909), Galerkin (1915), Trefftz (1926), Courant (1943), and then Hellinger und Reissner (1953). The methods presented vary in terms of their requirements regarding the trial functions that have to satisfy the differential equation or the boundary condition, or that can be freely selected. An intensive exchange with the University of California, Berkeley, was fostered within this field.

"Berkeley – home of the finite element method"
At Berkeley, researchers from many countries were on sabbatical through the 50s and 60s. The early research which did take place is described in the pages of a comprehensive publication [3], and this is briefly summarized below.
The initial idea of applying the force method – which Argyris had been applying to one-dimensional rigid frames (elements) – to two-dimensional elements, each of which would have three nodes and would assume a constant strain, was presented by Jon Turner, an engineer at Boeing, at a meeting of the Institute of Aeronautical Sciences in New York in 1954, but it was not published until 1956. Under Clough’s guidance, this idea was further developed by several students and then published at the 2nd ASCE conference in the form of a paper entitled: “The Finite Element Method in Plane Stress Analysis” [4]. The triangular element satisfied the stress strain relationship within the element, displacement compatibility between the elements, and force equilibrium at the nodes on an integral basis. This allowed two-dimensional structures to be divided into individual elements and assembled into a given overall structure while preserving both conditions of force equilibrium and compatibility. From a mathematical perspective, this led to a system of equations in which the displacement values at the nodes form the unknown quantity. Clough coined the term “finite element method” in the above-mentioned publication dating to 1960.
That same year, Clough and Wilson developed a fully automated finite element program that allowed engineers with little knowledge of mathematics to calculate plane (planar) structures of any geometry.
This set in motion a whirlwind of development. Modern methods of calculation were needed in the construction industry – for the purposes of upgrading freeway bridges and securing structures against the effects of earthquakes; for the manned space program (e.g., the moon landings in 1969); within the sphere of plant engineering for calculations relating to oil platforms and the Alaska oil pipeline, and in the construction of nuclear power stations, cooling towers, and dams. In order to facilitate these extensive research projects, a building (Davis Hall) was erected at the Berkeley campus for the Department of Structural Engineering. Developments were aided by the emergence of computers and the rapid increase in computer processing power.

Clough’s colleagues with expertise in continuum mechanics were skeptical about the new method. Among these was Professor Karl Pister, who set Clough a series of test calculations. The results all turned out to be satisfactory, and when more elements were added, they converged. In the course of further research, Pister then realized that the finite element method constituted a special formulation of the mathematics-based Ritz method (of 1909), an approximation-based variational method. In 1943, Courant had expanded the Ritz method to cover multiple domains (elements), however he had not pursued the method any further as it resulted in large systems of equations that were, at the time, insoluble. Other mathematicians who had developed approximation-based solutions based on the variational method were Galerkin (in 1915) and Trefftz (in 1926). They can be said to be forerunners of the finite element method – alongside Leibniz (1646-1716), who postulated that the variational method could be used as a means of solving arbitrary differential equations.
In structural mechanics, numerous elements of varying complexity were developed for use with planar structures, axisymmetric structures, plates, shells, and three-dimensional components. It was now possible to include geometric, material, and structural nonlinearities (contact zones), and various algorithms were compiled for the purpose of solving large systems of equations; and the method could be applied to other physic disciplines i.e. heat transfer or fluid flow.
With the collaboration of O.C. Zienkiewicz, Professor at the University of Wales in Swansea, and other researchers, the many and varied ways in which the method had been expanded were summarized and published in a series of papers in 1965 while Professor Clough was a visiting professor at the University of Cambridge, from 1964-65 [5]. In 1977, these summaries appeared in a book [6] together with a number of additions. In October 1965, the first international conference on “Matrix methods in structural analysis” took place at Wright-Patterson Air Force Base [7], bringing together scientists from many different countries. Since that point in time, the term “finite element method” has been widely accepted in preference to “direct stiffness method”.

Research at Berkeley proceeded in a variety of different directions
In the period 1965-1970, the research at Berkeley proceeded in many different directions, and this motivated numerous outstanding students to go to Berkeley, which was regarded as “the home of the finite element method”, with famous professors such as Clough, Wilson, Pister, Popov, Penzien, Felippa, Taylor, Bathe, Scordelis, and Bouwkamp – to name but a few – conducting their research here.
During this period, Wilson and Clough developed the SMIS (Symbolic Matrix Interpretive System) instructional software to bridge the gap between manual calculation and the matrix method. This was constantly updated, with the final version, CAL 91, still in use in 1999. In 1969, Wilson had created SAP (the Structural Analysis Program) for research purposes, and this was then updated by Klaus-Jurgen Bathe [8]. At the time, this version, SAP IV, was one of the fastest and most extensive programs available. It was available free of charge, which led to it being distributed throughout the world. At the end of his studies at Berkeley, back in 1977, the current author also took home a magnetic tape containing SAP IV.
In their closing passage, the authors of “Early Finite Element Research at Berkeley” highlight how the informal approach which prevailed at Berkeley, and which lacked any central direction, contributed to the successes. About 50 per cent of the students who were awarded their doctorates at Berkeley were appointed to professorships at major universities or gained positions at research centers within industry.
J.A. Argyris und R.W. Clough are today credited with having invented the finite element method and have received numerous awards. R.W. Clough and O.C. Zienkiewicz, who recognized the potentially broad applications of the finite element method, were honored with the Prince Philip Medal of the Royal Academy of Engineering, and J.A. Argyris was given the Einstein Award – one of the highest distinctions conferred in the United States.

Author
Dr.-Ing. Guenter Mueller, Founder of CADFEM GmbH and Managing Partner at CADFEM International GmbH
References
[1] Rannacher, R., Stein E.: Finite Elemente, Spektrum der Wissenschaften, März 1997, ISSN 0170-2971.
[2] Argyris, J.H.: Energy Theorems and Structural Analysis, Butterworths Scientific Publications, 1960.
[3] Clough, R.W., Wilson E. L.: Early Finite Element Research at Berkeley, Fifth U.S: National Conference on Computational Mechanics, Aug. 4-6, 1999.
[4] Clough, R.W.: The Finite Element Method in Plane Stress Analysis, Proc. 2nd ASCE Conf. On Electronic Computation, Pittsburgh, PA. Sept. 1960.
[5] Zienkiewicz, O.C.: Stress Analysis – Recent Developments in Numerical and Experimental Methods, John Wiley & sons Ltd., 1965.
[6] Zienkiewicz, O.C.: The Finite Element Method, McGraw-Hill Book Company, UK, 1977.
[7] Proc. Matrix Methods in Structural Analysis, Wright-Patterson Air Force Base, Ohio, October 26-28. 1965.
[8] Bathe, K.J., Wilson E.L., Peterson F.E.: “SAP IV” – A Structural Analysis Program for Static and Dynamic Response of Linear Systems”, EERC 73/11, Earthquake Engineering Research Center, June 1973.
The Evolution of Computational Mechanics
Stein, E.: Calculemus! The Craddle of Modern Science and Calculation Techniques in the 17th Century with Gottfried Wilhelm Leibniz as a Universal Scholar.
Stein, E.: The origins of mechanical conservation principles and variational calculus in the 17th century, GAMM Mitteilungen Volume 34, Issue 1 and 2, 2011, WILEY Verlag, Deutschland.
Mahrenholtz, O., Gaul, L.: Die Entwicklung der Strömungsmechanik von Archimedes bis Stokes und Reynolds, GAMM Mitteilungen Volume 34, Issue 1 and 2, 2011, WILEY Verlag, Deutschland.
Ramm, E., W. A. Wall: On the Evolution of Computational Mechanics – Personal Reflections, GACM Report, Autumn 2019, No. 12.
Wunderlich, W.: On the Development of Computational Mechanics in Germany and the Founding of GACM, GACM Report, Autumn 2019, No. 12.
Ramm, E.: Principles of Least Action and of Least Constraint, GAMM Mitteilungen Volume 34, Issue 1 and 2, 2011, Wiley Verlag, Deutschland.
Comprehensive summary of publications on computational mechanics
Stein, E., De Borst, R., Hughes, Thomas. J.R. (Editors): Encyclopedia of Computational Mechanics, 3 volumes, 2336 pages, John Wiley 6 Sons, Ltd., England, 2004.
Introduction to FEM theory
Bathe, K.-J.: Finite Element Procedures in Engineering Analysis, Prentice-Hall, Inc., Englewood Cliffs, New Jersey 07632, 1982, 1996, ISBN 0-13-317305-4.
© Images: private | Translation: Kieran Scarffe